Ibmec SP - Polígonos

 Ibmec-SP - Suponha que você disponha de uma quantidade infinita de cópias de uma determinada forma geométrica. Se for possível encaixá-las, sem falhas ou sobreposição, de modo que o plano seja todo coberto por elas, dizemos que essa forma geométrica pavimenta o plano. No ano de 1968, o problema de pavimentar o plano com pentágonos convexos idênticos parecia resolvido: aparentemente, apenas oito tipos de pentágonos convexos possuíam essa propriedade. Porém, um acontecimento surpreendente causou uma reviravolta no problema. Uma dona de casa americana, Marjorie Rice, cuja formação matemática limitava-se àquela obtida no ensino médio, tomou conhecimento do assunto em uma revista de divulgação científica e descobriu, entre 1976 e 1977, quatro novos tipos de pavimentações do plano usando pentágonos convexos.

A figura abaixo mostra um dos tipos de pavimentação do plano descoberto por Marjorie Rice.

Nesse caso, o pentágono convexo ABCDE satisfaz as seguintes condições:

Observando-se a figura da pavimentação, pode-se concluir que esse pentágono também satisfaz a condição:

Bom, nos é fornecido várias informações, mas primeiro temos que calcular quanto é a soma dos ângulos internos de um polígono:

n = número de lados

Como todos os ângulos somados são 540º, vamos escrever isso assim:

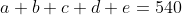
 (1)

Cada letra representa um ângulo, agora, nós já temos algumas informações do próprio enunciado, então, vamos isolar as letras E e D nas equações que nos foi fornecidas:





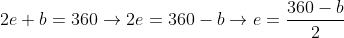
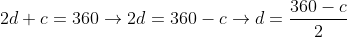
Agora vamos substituir na equação (1) e fazer as contas:



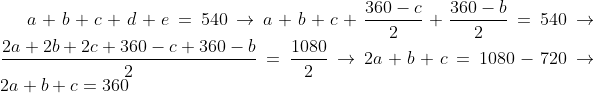
Portanto, 2A + B + C = 360º, alternativa A.