ACAFE - Conjuntos

ACAFE SC 2012_1 MEDICINA -  Sobre os conjuntos abaixo, analise as afirmações a seguir:

A = {x ∈ N* / x < 200}
B = {x ∈ A / x é múltiplo de 8}
C = {x ∈ A / x é múltiplo de 3}


I - O conjunto BUC possui 90 elementos.
II - O conjunto C possui 65 elementos.
III - O conjunto dos múltiplos naturais de 3 e 8 menores que 200 possui 8 elementos.
IV - A soma dos elementos contidos em AUB é igual a 8169.

Assinale a alternativa correta:

a) Todas as afirmações são verdadeiras.
b) Apenas a II e a III são verdadeiras.
c) Apenas a afirmação III é verdadeira.
d) Apenas III e IV são verdadeiras.


Primeiro vamos analisar os dados que foi fornecido, ele diz que o conjunto A tem elementos de 1 até 199, e dentro desses números estão o conjunto B, que é só com múltiplos de 8, e o conjunto C, que é só com múltiplos de 3.

Vamos ver quantos elementos tem no conjunto B: são os múltiplos de 8 compreendidos entre 1 e 199. Podemos formar uma P.A de razão 8 para descobrir quantos tem, então:


a1 = 8
an = 192
r = 8

an = a1 + (n -1).r
192 = 8 + (n - 1).8
192 = 8 + 8n - 8
192 = 8n
n = 24

O conjuntos B tem 24 elementos.

Agora vamos fazer o mesmo para o conjunto C, que são os múltiplos de 3 entre 1 e 199:

a1 = 3
an = 198
r = 3

198 = 3 + (n - 1).3
198 = 3 + 3n - 3
198 = 3n
n = 66

Então o conjuntos C tem 66 elementos.

Ele pede na alternativa I a união de B e C, mas existem números que são tanto múltiplos de 8 e de 3 ao mesmo tempo, então temos que eliminar esses para não haver números repetidos. Múltiplos de 3 e 8 são múltiplos de 24, então:

a1 = 24
an = 192
r = 24

192 = 24 + (n - 1).24
192 = 24 + 24n - 24
192 = 24n
n = 8


Então, união de B e C: 24 + 66 - 8 = 82 elementos. Alternativa I está falsa.
A alternativa II também está falsa, o conjuntos C tem 66 elementos, já foi calculado acima.
A alternativa III está certa, também já foi calculada acima. (múltiplos de 24)

Para fazer a alternativa IV temos que descobrir a soma dos termos dos conjuntos A e B, então:

Conjunto A: a1 = 1
an = 199
n = 199

Sn = (a1 + an).n/2
Sn = 200.199/2
Sn = 19900

Só por este valor já está claro que não pode dar 8169, então alternativa falsa.

Gabarito: letra C.

ACAFE - Trigonometria

ACAFE SC Prova de Medicina Verão 2014: Com o objetivo de auxiliar os maricultores a aumentar a produção de ostras e mexilhões, um engenheiro de aquicultura fez um estudo sobre a temperatura da água na região do sul da ilha, em Florianópolis. Para isso, efetuou medições durante três dias consecutivos, em intervalos de 1 hora. As medições iniciaram às 5 horas da manhã do primeiro dia (t = 0) e os dados foram representados pela função periódica , em que t indica o tempo (em horas) decorrido após o início da medição e T(t), a temperatura (em ºC) no instante t.
O período da função, o valor da temperatura máxima e o horário em que ocorreu essa temperatura no primeiro dia de observação valem, respectivamente:

a) 6h, 25,5ºC e 10h
b) 12h, 27ºC e 10h
c) 12h, 27ºC e 15h
d) 6h, 25,5ºC e 15h

Essa questão envolve conhecimento de funções trigonométricas, nesse caso a função cosseno. Primeiro ele pede o período da função, então vamos calcular:

Período da função cosseno é: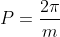 , sendo M o valor que fica na frente de "x", que nesse caso é t, então m é o que está na frente de "t".



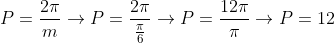
O período da função vale 12, então já eliminamos as alternativas A e D.

Para calcular a temperatura máxima temos que fazer a imagem do cosseno, e como o valor máximo, temos que considerar o valor máximo do cosseno, que é 1. Então basta trocar o "cos" na função pelo número 1.

T(t) = 24 + 3 . 1 = 27 ºC

Agora temos que calcular o horário que ocorreu essa temperatura, ou seja, o horário em que o valor de cosseno foi máximo. Então valor igualar o cosseno a 1:



Os lugares nos quais o cosseno valem 1 são: 0º ou 360º. Como o 0º não pode, vamos usar o 360º, que passando para radianos é 2pi.



Então, desde o início das medições se passaram 10 horas até a temperatura máxima, e como o enunciado diz que as medições começaram as 5h da manhã, a temperatura máxima irá ser obtida as 15h da tarde.

Portanto, alternativa correta letra C.